フェルマーの最終定理 350年越しの数学ドラマ 2/3
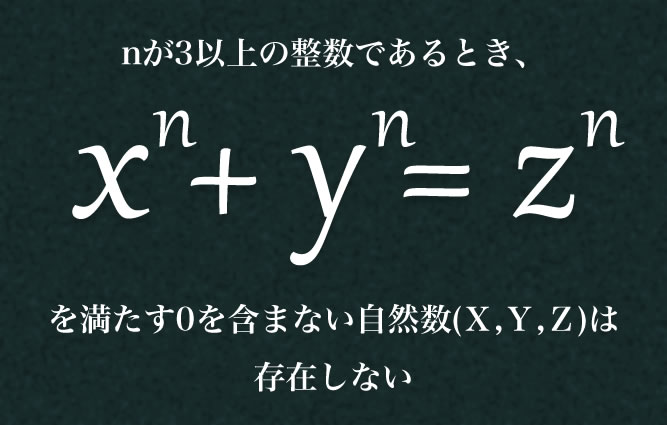
皆様、いかがお過ごしであろうか? 数学はできてもお金の計算がおろそかな野地である。
家計簿一つつけない自分が悪いのは百も承知なのだが、電気代の支払いがずれて二か月分一気に請求されるなど誤算にもほどがある。
しかし多分、そういう失敗にめげず、トライ&エラーを繰り返せる人間こそが成功を掴むのだろう。とりあえず、現実を見て今晩の夕飯はもやしにしよう。
さて、今回はそんなトライ&エラーの権化と言っても過言でない、やがて世界で一番有名な数学者の一人となる人物の登場までを紹介しよう。
古典的なアプローチでは既に解決不可能であることを悟った数学会が新たに生み出した現代的アプローチの登場とともに、フェルマーの最終定理をめぐるドラマが加速していくのを楽しんで欲しい。
目次
今回は中盤、谷山=志村予想の登場からアンドリュー・ワイルズの研究が始まるところまでを紹介したいと思う。
現代数学の最終兵器、谷山・志村予想登場
しばらく眠っていたフェルマーの最終定理だが、全く関係のないところでそれを叩き起こす事件のきっかけが生まれた。
1955年9月に日光の国際シンポジウムで、若い二人の日本人数学者が衝撃的な予想を発表したのだ。
戦後間もない日本の学問界では、戦中に西洋の学問を十分に吸収できなかったことに加え、実験に使う器具や施設の準備がままならないこともあり停滞気味であったらしいのだが、数学は基本的に(コンピューターによる計算も導入され始めていたとはいえ)紙と鉛筆さえあれば研究できる。
そこで勉強意欲の凄まじい学生たちは、時代遅れとなった問題に取り組むこともあれど、着実に、時に独創的なひらめきをもって数学を研究していた。
そんな中、当時まだ20代であった谷山豊と志村五郎によって発表されたのが「谷村=志村予想」である。
その内容は「すべての有理数体上に定義された楕円曲線はモジュラーであろう」というものだ。
超ざっくばらんに説明すると、まず楕円曲線とは
y^2=x^3+αx+β
の形で表される方程式で、このαやβの値を変えてやることによって、全く振る舞いの異なるこの方程式である。楕円曲線という名前は、この方程式自体が楕円を描くわけではなく、かつて正円ではなく楕円を描くことが明らかになった惑星運動の計算に用いられたことがこの名称のきっかけだったようである。
対して、モジュラー形式とは、数学界でも最も奇妙な概念の一つであり、説明が非常に難しい。
よく言われる例えが、「数学には5つの基本演算があり、それは加法(足し算)、減法(引き算)、乗法(掛け算)、除法(割り算)、そしてモジュラー形式である」というものである。
これだけでモジュラー形式というモノの深さは感じてもらえたと思うが、もう一歩踏み込んで説明すると、モジュラー形式最大の特徴はその「対称性」にあるとされる。
あるモノを「変換」するとそのモノは違ったモノへと変化するわけだが、ときどき、「変換」をしても変化しないことがある。
このような場合を数学で「対称性を持っている」という。
例えば、正方形は90°回転させても、180°回転させても変化しない。
無限に続く1cm×1cmのタイル張りは上下左右どの方向に1cm動かしても変わらない。
0という数字はどんな数を掛けても0のままである。
等々、対称性をもつ場合は色々あるのだが、モジュラー形式はこのような対称性を驚くべき精度で持っているということなのである。
さらにさらに踏み込むと、まず中学生辺りで習ったであろうx軸とy軸が十字に交差するあの図を思い浮かべて欲しい。
あの上で二次関数(U字のあれ)やら円(三角関数のあれ)やら波(正弦波とか)を表せるのだが、モジュラー形式も二本の軸で表すことのできる概念である。
ただし、その二本の軸は+-含めた実数ではなく、α + βi (i = √-1)で表される複素数による軸であり、一本の軸で実数部分と虚数部分を持つため理解が一気にややこしくなるのだ。
さて、一見何の関係もなさそうなこの二つを繋げる架け橋が「谷村=志村予想」だ。
事実、楕円曲線は前章で登場したディオファントスの時代から研究されていたのに対し、モジュラー形式は19世紀に入ってやっと確率した概念であり、その二つを比較しているこの予想は数学界に衝撃をもって迎えられる。
谷山と志村は予想の根拠を実例としていくつか挙げていたようだが、数々の数学者による研究でその実例以外の場合もどうやら谷村=志村予想は正しいようだった。
そして次第に、どの数学者も実例と直感で谷村=志村予想は正しいと思うようになり、数論の分野で発表される論文に「谷村=志村予想が正しければ」という一文がよく登場するようになる。
なぜなら谷山=志村予想が正しいとするのであれば、モジュラー形式側から解こうとすると不可能に思われた問題も、そのモジュラー形式を等価の楕円曲線に変換し、楕円曲線側からのアプローチで問題を解決することができるからだ(逆もまたしかり)。
しかし、数学の世界において予想は定理よりずっと価値が低い。
定理は一度証明すれば永遠に真であり、その定理の上に安心して数学のさらなる発展を積み上げることができる。
対して予想はまだ抜け漏れが無いことを保証できないものである。その予想がいかに有用なものであっても、その予想に依存して作られた理論は砂上の楼閣であり、その予想の反証が明らかになった瞬間、全てがゴミになってしまうのだ。
前述の通り、数々の数学者は谷山=志村予想を恐らく正しいと思っていたが、その証明はほとんどの人間が絶望視していた。
そしてある日、谷山=志村予想の発展を見ないまま、その生みの親である谷山が自殺してしまう。
遺書には「何かある特定の事件乃至事柄の結果ではない」と書かれており、直接のきっかけがあったわけではないようだが、「ただ気分的に云えることは、将来に対する自信を失ったということ」と続けられている通り、生きるに堪えない重大ななにかがのしかかっていたのは事実であるようだ。
しかもその二週間後、谷山の婚約者であった女性も後追い自殺でこの世を去る。
当時の数学者たちにこの悲しい報せはすぐに届いただろう。数学者が自分の仕事のことを存分に語れる仲間は数学者だけなのである。誰がいなくなろうと朽ちない物を作る代わりに、それを生み出す人間はそう簡単に表れない。多くの数学者が喪失感を感じていたはずだ。
しかしそんなムードの中、既に多くの城の土台になっていた谷村=志村予想の上に、特大の城が建てられることになる。
なんと、谷山=志村予想が正しければフェルマーの最終定理も正しいと証明できることが明らかになったからである。
フェルマーへと架けられた橋
その種を最初にまいたのはドイツのゲルハルト・フライという数学者である。
彼は先述した谷山=志村予想に穴がないかを調べていた。
楕円曲線をこねくり回して、それがモジュラー形式ではない例が一つでも現れれば谷村=志村予想は正しくないことになる。フライはそのケースに当てはまりそうな楕円曲線を色々と考えていたのだ。
そうした研究の末にフライが思いついたのが「フライ曲線」である。
それは存在すれば確かにモジュラー形式に変換できない曲線なのだが、この曲線が存在するには前提条件が必要だった。
実はその前提条件を少々変換すると、「フェルマーの最終定理が間違っていれば」という意味になる。
つまりこのとき初めて、最終目的としてのみ存在してきたフェルマーの最終定理が、他の問題に付随して証明される形で世に現れたのである。
この式はその後ジャン=ピエール・セールという数学者によって定式化され、フライ・セール予想として世に出ることになった。
さて、この予想は前回の記事で紹介したディオファントスがよく用いたとされる「背理法」と呼ばれる強力な方法が用いられている。
背理法とは、ある問題が偽である(間違っている・嘘である)と仮定した後、その仮定を使って導き出される結果が事実と矛盾していることでその問題は真である、と結論付ける問題の解き方である。
よくある話に例えると、
- 過去へ戻れるタイムマシンは未来に存在するとする
- 過去へ戻れるタイムマシンがあるならば、今現在の世の中にも未来からやってきた何かが残した痕跡があるはずである
- 現在、そのような証拠は見つかっていない
- つまり、過去へ戻れるタイムマシンは未来に存在しない
といった具合である。
勿論、この話で言う所の「未来からやってきた何かが残した痕跡があるはず」というのは現代のテクノロジーではわからない痕跡の消し方を未来人が持っている、等の抜け穴がいくらでもある。
しかし、そんな現実世界とは違い数学の世界における定理には一部の隙もない。
一度「真」とされた定理が「偽」となってしまうのであれば、それは定理自体の問題ではなく、その前提条件が間違っているということが誰でも自信をもって言い切れるのである。
このように既存の定理を用いて新たな証明を増やしていく背理法は数学界の歴史上で様々な成果をあげてきたのは言うまでもないが、特筆すべきはその背理法が得意とする相手だ。背理法は特に、「無限のケース」を持つ問題に効果的な方法なのである。
前回の記事で紹介した悪魔の証明を思い出してほしい。
それが「無い」ということを証明するのは、それが「有る」ということを証明するのに比べ遥かに難しい。なぜなら、それが「無い」ことを証明する範囲が「無限」だった場合、その範囲を総当たりで検証していく証明方法は不可能になってしまうからである。
しかし、背理法はまず前提条件を否定してから証明を組み立てる方法だ。
背理法を悪魔の証明に当てはめてみよう。それが「無い」という条件を否定するという事はそれが「有る」ということに等しい。
つまり前提条件が逆の意味になり、遥かに難しかった問題が、遥かに簡単になるのである。
フライ・セール予想に話を戻そう。フライ・セール予想の筋道はこうだ。
フェルマーの最終定理が偽である(X^n+Y^n=Z^nが成り立つ自然数X,Y,Zが存在する)と仮定する
X^n+Y^n=Z^nを変形して、モジュラー形式に変換できない楕円曲線を作ることができる
しかし谷村=志村予想が正しければ、モジュラー形式に変換できない楕円曲線は存在しない
これは谷村=志村予想に矛盾している
つまり、前提条件であるフェルマーの最終定理が偽であるのは誤りで、フェルマーの最終定理は真である
フェルマーの最終定理もまさしく「無限のケース」を持つ問題であり、それが背理法として証明できるという事実は多くの数学者を興奮させたに違いない。
だがその一方でこんな感想を持つ数学者もいただろう。「ただでさえ証明の絶望的な谷村=志村予想が、300年以上証明できないフェルマーの最終定理に結びついてしまったんだ。やはり、谷村=志村予想は到底手に負えるものではなかったのだ」
無謀者
フライ・セール予想はその後、ケン・リベットという数学者によって完璧に証明された。
この魅力的な予想を証明できれば、現代数学は一気にフェルマーへと近づくこととなる。
リベットはこの証明である一か所の部分を除いてほぼ証明が終わっていたが、どうしてもその最後一手が解決できずにいた。
ある日のこと、バリー・メイザーという数学者と一緒にアイスティーを飲んでいたリベットはメイザーにその苦戦している証明の話をした。
するとメイザーは、なんと一瞬でその解決方法を言い当ててしまった。
リベット自身も、なんでそんなシンプルなことに気付かなかったのだろうと後に語っているが、それは日常の些細な問題とは一線を画す難解な数論の世界の話である。よく、深く考えても解けない問題は俯瞰して全体を見回たすのが良いと言われるが、ちょっとでも距離を離すと見えなくなってしまうほど目の細かい網が相手では、なかなかそうもいかないのが実際の現場なのだろう。
現代数学の世界では情報が回るのは早いらしく、この証明は即座に世界の数学者の知るところになった。
ただ、その報せがどんなに魅力的であっても、その鍵となる予想は難攻不落の谷村=志村予想である。
フェルマーへと橋が架けられたといっても、その橋は本当にあるのだろうか?
その、もし存在しなかったら奈落の底へと落ちてしあうであろう橋を渡る者はほとんどいなかった。そんなことをする数学者はもはや山師であるか、無謀者だけである。
さて、無謀者とは決して勉強のできない者とは限らない。むしろ、頭の良い人物ほど無謀な人間は多いかもしれない。
だいたい、大きな成功を収める人間の半分は無謀者の一面を持っているのは誰でも経験的に分かることだと思う。
そんな無謀者がプロの数学者にも、少なくとも一人は居た。当時、楕円曲線論の研究で最先端を突き進んでいたイギリスの数学者、アンドリュー・ワイルズである。
夢に歩み寄る、夢も歩み寄る
ワイルズはその時既に、確かな実績を上げている天才数学者だった。
前述した楕円曲線論を専門にしており、彼の指導を行ったジョン・コーツやバリー・メイザーと共に名の残る仕事をしている。
そのままでも恐らく今世の大学生読む教科書に名前が載るくらいの業績があったわけだが、そんな彼でさえ胸の奥にしまいこんでいる夢があった。その夢の発端は彼が10歳の頃にまで遡る。
ある日、彼は図書館で一冊の本に出合う。
そこに書いてあったのがフェルマーの最終定理だったわけだが、その問題の言わんとしていることは10歳だった彼も容易に理解できた。
しかし、その本の結びにはその証明を解いたものは300年誰一人としていない、と書かれているのを見て、ワイルズはこの問題は自分が解かなければならないと感じたという。
そんな夢を抱えたまま数学を勉強し続けたワイルズは、いつの間にか実績ある天才数学者となっていた。
しかし、夢見る少年からプロの数学者となった彼は、その夢を胸の奥にしまい込んでしまう。
相手はなんといってもあのフェルマーである。人類が総出で掛かっても未だ解かれない問題に、人生を潰すわけにはいかなかったのだ。
これはワイルズ個人だけの問題ではなく、少々スケールを大きく言えば数学界の問題だ。ワイルズほどの貴重な頭脳を、この解けるかも分からない問題にあてがうのは、許されないことだったのである。
そんなわけで、ワイルズはフェルマーの最終定理とはなんら関係のなさそうに見える楕円曲線論と岩澤理論の研究を進めていた。
岩澤理論とは、日本人数学者の中でも早期に国際的な数学者となった岩澤健吉の生み出した理論で、今日でも数論の中心に位置する理論である。
岩澤がもたらした数論の理論は現代数論になくてはならない理論であり、最先端の数論を研究していたワイルズも岩澤理論を駆使する数学者の一人だった。
岩澤理論と楕円曲線論に関して、ワイルズは当時、世界のトップを走っていたのである。
しかし、運命のいたずらか、そんなワイルズの耳にもケン・リベットの証明のニュースが飛び込んできた。
誰もが全く関係に気付いていなかった、全く他分野と思われていた楕円曲線、モジュラー形式、そしてフェルマーの最終定理。
その三つが結ばれたというニュースに、ワイルズはさぞ興奮したことだろう。
自分の専門分野が、諦めていた子供の頃の夢に続く架け橋となったのである。
秘密の研究部屋
だがワイルズにとって、谷にかかる橋の両山のうち片方は自分の縄張りであるが、もう一方の山であるモジュラー形式は未だ見ぬ土地であった。
もちろん、並みの一般人や大学生よりは確実に高い位置まで登った経験があるだろうが、プロの世界とは一つの分野を極めれば極めるほど過酷な道を進む必要がある。最新技術というモノは先駆者が少ないだけに資料も少なく、獣道を進むうちにとうとう自分しか踏み入ったことのない領域へと道を開拓してしまうのだ。
いくら広いくくりで数学者というプロであっても、門外漢の分野で新たな開拓者になるのは膨大な根気と時間が必要だ。
数学者という職業はオールタイムジョブ(24時間仕事)と言われる類のモノではあるが、それで一生をかけたとしても、絶対に尽きることのない深さを持っているのが数学である。
ワイルズは再び子供の頃の夢へ向かう決意をした。
しかし、仕事の片手間では自分の人生で間に合うかどうか分からない。
そこでワイルズは大学院教授として最低限の仕事をこなしながら、自宅の屋根裏部屋に引きこもる生活を始める。そして、そこで手始めにモジュラー形式についての猛勉強を始めるのだった。
さて、この時点でワイルズが特徴的な点は、誰の手助けをも借りない独力での研究を選択した点である。
それこそオイラーやガウスらが活躍した時代においては一人での研究が多かっただろうが、仕事というのは効率を求めれば求めるほど分業化が進むものだ。
事実、ワイルズの活躍する現代的な数学者の仕事は共著によるものが多く、各分野の専門家が集って一つの問題を解決するスタイルが一般的になりつつあった。
データは電子メールも一般的になりつつあった時代なので、ワイルズ一人でも集め切れただろう。
しかし、そのデータの使い方、特にモジュラー形式に関する部分をその分野のプロに頼むのではなく、時間がかってもワイルズはそれを勉強し、あくまで一人でフェルマーに挑んだ。
なぜなら、共著になればその手柄は貢献度具合で分けられたものになってしまうからである。
ワイルズは「一人」でフェルマーに打ち勝ったという名声が欲しかったのだ。
一見、この功名心は汚く感じるかもしれない。
しかし、金、地位に興味がなくとも、学問的名誉に興味の無い数学者など本当の本当に一握りである(ペレルマンとかが例外に当てはまるだろうか)。
しかも、その成果物がフェルマーの最終定理ともなると、これはもはや人類の歴史に残るといったスケールの話ではない。一般の人間にはフェルマーの最終定理が解けたという事実だけが印象に残るかもしれないが、それはあくまで副産物であり、それよりも楕円曲線論とモジュラー形式が結ばれるということは細分化の激しい数学界の、まさに数学者が夢見た大統一理論への第一歩となりうるのだ。
だがそれが複数人での仕事となるならば、名誉は山分けどころか、研究の途中段階で自分以外の誰かがそれを漏らし、最後の王手だけを他人に果たされることになりかねない。どの業界でも最後の一手をやった者勝ちであるのは変わらないのである。
だからこそ、ワイルズはフェルマーという強敵を相手取りながらも、一人で戦うことを決めたのである。
ワイルズの隠遁生活は既に発見していたがまだ発表していなかった研究を小出しにしつつ、彼の妻のみがフェルマーに挑むことを知るまま続けられた。
まとめ
現代数学におけるフェルマーへのアプローチ、いかがだったろうか。
自分を含め、難解すぎて理解ができないような理論の話も出てきたが、あの簡単そうな式一つを証明するのにここまで巨大な道具を持ち出さねばならないのは、なんともロマンの溢れる話に感じる。
次回は最終回、アンドリュー・ワイルズを中心としたフェルマーの最終定理というドラマの大詰めを紹介したいと思う。
是非是非、最終回まで楽しんでいって欲しい。
Comments
-
-
Oi, looking to snag the Superbet app, eh? Heard it’s pretty slick. Makes placing your bets on the go dead easy. Download’s straightforward enough. Here’s the link: superbet download
-
42vipph is giving good vibes recently. The game selection is extensive, and the support team is helpful. Pretty straightforward to navigate, too. 42vipph
Warning: Undefined variable $aria_req in /var/www/html/noji.dev/wp-content/themes/ODD_CODES/comments.php on line 15
Warning: Undefined variable $aria_req in /var/www/html/noji.dev/wp-content/themes/ODD_CODES/comments.php on line 17

長文お疲れ様です。とても興味深い話でした。これからも更新頑張ってください。